A very common question math faculty get is about the content of Math 124 Finite Math. Unfortunately, no simple answer can be given in twenty-five words or less. But that's why you are reading this, yes?
"Finite Math" is a catch-all title for a collection of topics that are anything but calculus. The purpose of the course is to give a survey of mathematical analysis techniques used in the working world, but you might also say that this course gives valuable experience at organizing information and then analyzing it. In a larger sense, it's also another way we use math to give people experience at analytical thinking. Business, accounting and computer majors tend to take this course, or are required to by their program. It is an excellent choice for many education majors to fill their math requirements, but these people should check with their transfer institution first.
Here is a list of the main topics covered:
-Mathematical model building. Math modelling is the act of creating functions or equations that describe a given application or situation. In this course we mainly concentrate on business-oriented ideas such as break-even analysis or depreciation.
-Matrix algebra. Matrices are collections of numbers organized in rectangular arrays. These can effectively represent certain kinds of data or systems of equations. In Finite Math you only get a brief glimpse into how they are used and manipulated, but matrix ideas can arise in both accounting and business analysis, and computer programmers use them as array variables.
-Linear programming. This topic has nothing to do with computer programming, but it is a method for optimizing situations when constraints are in place. For example, if you produce several lines of products but have budgetary constraints on labor and materials, and have production contracts in place that must be filled, then what is the most efficient, profitable way to determine how much of each line to produce, that is, how can you maximize the profit potential? Linear programming is ideally suited to problems of this nature. Linear programming can also be an application of both math modeling and matrix algebra.
-Combinatorics. This is the art of advanced counting. For example, if a room has twenty chairs and twelve people, in how many ways can these people occupy the chairs? And are you accounting for differences in who sits in particular chairs, or does it only matter if a chair has a body in it? These kinds of counting problems are the basis for . . .
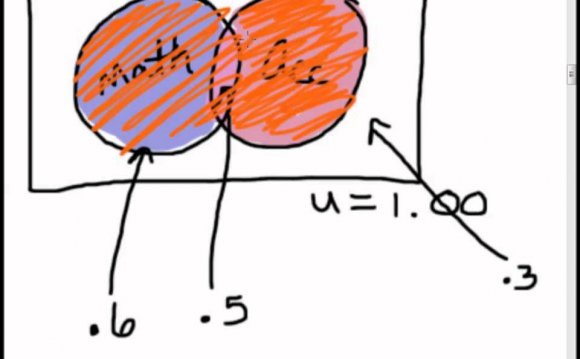
-Probability. In order to calculate the chance of a particular event happening you must be able to count all the possible outcomes. Once you understand how to find probabilities then you can begin to understand . . .
-Statistics. Statistics uses probability in order to analyze data and make decisions. In Finite Math you will only get a brief introduction and overview of statistics. For information about the subject you can link to:
-Logic. Logic is the symbolic, algebraic way of representing and analyzing statements and sentences. You will only get a brief introduction to logic in this course, but the mathematics used in logic are found at the heart of computer programming and in designing electrical circuits.
More advanced courses in Finite Math topics are sometimes called Discrete Mathematics. The word discrete helps explain where Finite Math gets its name. Discrete means broken up or separated. For example, integers are discrete objects because there are non-integer numbers in between them, but real numbers are continuous numbers because there is no identifiable separation between them.
For a maddening exercise in continuity try finding the largest real (i.e., decimal) number less than one. No, it is not 0.999999 . . . (the nines repeating forever), because it can be demonstrated that 0.999999 . . . is equal to 1. Whatever this number is it is impossible to represent it in any other than the most abstract way.
Continuity is in some ways associated with infinity and infinitesimal. Since calculus is concerned with continuous numbers and continuous functions, the subject must confront the ideas of infinity and infinitesimal. Finite Math is a subject that avoids the issues of continuity encountered in calculus, so those topics are lumped into the category of "finite mathematics."
INTERESTING VIDEO